完成《基于函数秘密共享的高效电子投票方案》项目后的一点思考。
参考文章:函数秘密分享(二) - 知乎 (zhihu.com)
伪随机生成器PRG:PRG是一个密码学工具,它的输入是一个安全参数 λ 长度的种子,并且输出看起来随机串。DPF使用的是长度加倍的PRG,它的输出是输入的两倍,需要调用两次AES加密,第一轮用于生成中间伪随机序列,第二轮用于加密中间伪随机序列,生成最终的双倍长度的伪随机串。
在项目中使用到 PRG 的地方:
sL∥tL∥sR∥tR=G(s(j−1))
这里产生的伪随机串并不是刚好的双倍长度,而是2(λ+1)。写代码时偷懒了用的也不是AES,而是直接用线性同余法生成伪随机串。
我们要在生成算法中构建给到两方的密钥。最开始给定两个不同的随机PRG种子,根据这两个种子会构建出两棵不同的伪随机函数的树。我们的目标是去秘密分享在所有其他地方都几乎相等,只要在特定点函数alpha路径上才不同的函数。为了达到这个目标,我们需要构建每一层的纠正词CW, 只要你离开与特殊值不一致的路径,它就会以某种方式强制两边相等。
这也是为什么对于无效的选票(β=0)可以直接令两边的份额为相等的随机串,这样两边都是一样的,即都是错误的路径,不会得到结果。
这个alpha路径在项目里就是这张选票所投的候选人的ID,将其分解为 n 位的比特,0代表向左走,1代表向右走。(有 η 位候选人,n=log2η)
初始:s0={0,1}λ,s1={0,1}λ,t0={0,1},t1=t0⊕1
分析alpha路径上的某一个节点,那么当双方拿到种子和随机比特的分片后:
- 每一方根据自己拥有的种子分片,利用PRG做扩张,然后将这个串分成左半部分和右半部分。
sL∥tL∥sR∥tR=G(s(j−1))
- 在上一步扩张的基础上,我们的目标是想要去构建纠正词CW。我先直接给出构造方法,在后续 Eval 部分会验证这个构造方法的正确性。
scwtcwLtcwRCW(j)=s0Lose⊕s1Lose=t0L⊕t1L⊕αj⊕1=t0R⊕t1R⊕αj=scw∥tcwL∥tcwR
- 更新 s 与 t。
s(j)t(j)=sKeep⊕(t(j−1)⋅scw)=tKeep⊕(t(j−1)⋅tcwKeep)
在 Eval 部分,纠正词应该使得错误分支上两边更新的 s 与 t 是相同的,而正确分支上 s 是不同的随机串,t 相反的比特。
分析结束后还需要将一个 1 掩盖起来(正常情况下 β=1 ):
CW(n+1)=(−1)t1⋅[β−ConvertG(s0(n))+ConvertG(s1(n))]
ConvertG:是将长度为 λ 的比特串映射为群中一个元素的映射算法。
在这个项目里,又偷懒了一下,直接没有进行映射。
在 Eval 部分,错误路径的 y 相加为 0 ,而正确路径上掩盖的 1 可以被解码出来得到 y 相加为 1 。(后面会进行分析, y 是 Eval 部分中的一个变量,两边相加的结果是 1 则该选票投给了这个选民)
该项目后面还进行了一些操作,是为了进行一些验证,和函数秘密共享没啥关系,就不在这里进行分析了。
最后的函数份额是这样的:
kb=sb(0)∥tb(0)∥CW(1)∥CW(2)∥⋯∥CW(n+1)∥cs∥pos
遍历每一个候选人ID沿着伪随机函数的树向下走。
如果两方在alpha路径某一节点上,每方拥有一些伪随机串和比特,它们拥有的串是随机的,比特是相反的。每一方根据自己拥有的串,利用PRG做扩张,然后将其分成左半部分和右半部分。
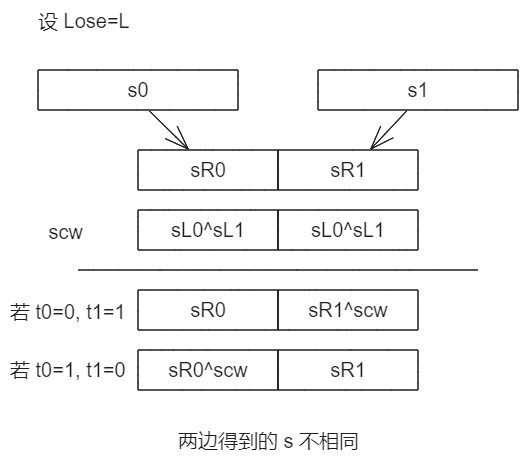
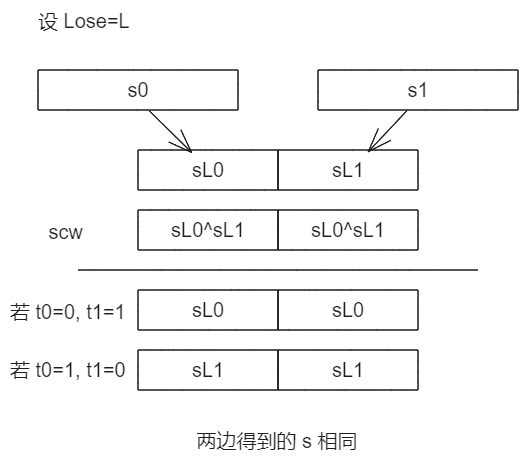
对于错误分支,控制比特为 0 的一边更新时不异或 scw 仍为 sLose,而控制比特为 1 的一边更新时异或 scw,sbLose⊕sbLose⊕sb⊕1Lose,异或自身等于 0 则 s 更新为了与另一边相同的 sLose。
 ::
::
而正确路径上不会出现异或自身的情况,所以不会得到另一边的 sKeep,因此两边就不会相同。
t 得到另一边 tLose 的方法与 s 并不一样,是因为需要保证在正确分支下产生的 t 需要相反。
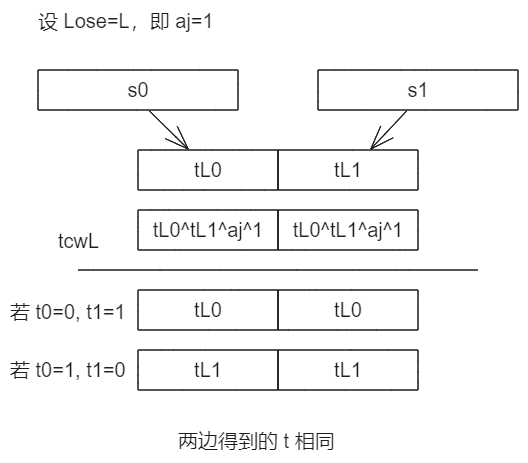
在 αj=0 时,错误分支是右侧的,tcwR=t0R⊕t1R⊕0=t0R⊕t1R。
在 αj=1 时,错误分支是左侧的,tcwL=t0L⊕t1L⊕1⊕1=t0L⊕t1L。
因此对于错误分支依旧有,控制比特为 0 的一边更新时不异或 tcw 仍为 tLose,而控制比特为 1 的一边更新时异或 tcw,异或自身等于 0 而得到另一边的 tLose 。
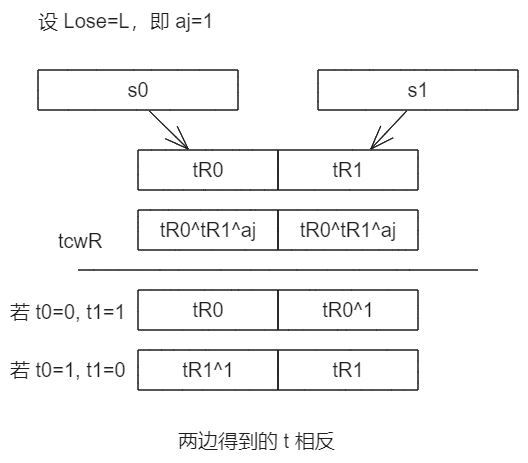
在 αj=0 时,正确分支是左侧的,tcwL=t0L⊕t1L⊕0⊕1=t0L⊕t1L⊕1。
在 αj=1 时,正确分支是右侧的,tcwR=t0R⊕t1R⊕1。
因此对于正确分支,控制比特为 0 的一边更新时不异或 tcw 仍为 tKeep,而控制比特为 1 的一边更新时异或 tcw,得到另一边的 tKeep⊕1 ,保证了新的控制比特依旧相反。
如果已经不在 alpha 路径上了,那么 s0=s1 且 t0=t1,然后两边会进行一模一样的运算从而更新出下一轮一模一样的 s 与 t。
在前面部分最后一个纠正词 CW 把 β 掩盖了起来:
CW(n+1)=(−1)t1⋅[β−ConvertG(s0(n))+ConvertG(s1(n))]
接下来还要将其解码出来:
yb=(−1)b[Convert(s(n))+t(n)⋅CW(n+1)]∈G
如果走的是错误的路径,那么两边的 s 与 t 是相等的,则计算出来的 y 一定会相加为 0 。
如果走的是正确的路径,假设 t0=0,t1=1,那么:
y0+y1=Convert(s0(n))−[Convert(s1(n))+CW(n+1)]=Convert(s0(n))−Convert(s1(n))+β−Convert(s0(n))+Convert(s1(n))=β
这样就可以知道正确路径对应的候选人获得了一票。
 ::
::