一、语言

用以描述计算机所执行的算法的形式表示。

由语法和语义组成。

1. 语法

用以构造程序及其成分的一组规则的集合。（定义语言是否合法的一组规则）

几个术语

• 字母表：语言允许使用字符的集合，其元素称为字符；由字符组成的有限串（字符串）称为符号
• 字汇表：由符号组成的集合，其元素称为字
• 词法规则：规定什么样的字符串可以构成语言的有效符号
• 语法规则：确定一个符号序列是否为一个句子，并提供句子的结构

生成的观点：产生式

文法$G=(N,T,P,S)$，其中

$$\begin{aligned} N= & V_N \\ T= & V_T \\ P= & \text{产生式的集合} \\ S= & \text{文法开始的符号} \end{aligned}$$

Note

产生式一般写为$\alpha\rightarrow\beta$，其中$\alpha\in V^{*}V_NV^{*}$，$\beta\in V^{*}$，$V=V_N\cup V_T$。

一般情况下，文法指的就是P。

# 标识符的文法
<标识符> -> <字母>
<标识符> -> <标识符><字母>
<标识符> -> <标识符><数字>
<字母> -> A|...|Z|a|...|z
<数字> -> 0|1|...|9

# 表达式的文法
<表达式> -> <标识符>
<表达式> -> (<表达式>)
<表达式> -> <表达式><运算符><表达式>
<运算符> -> +|-|*|/

识别的观点：语法图

语法图的定义：每一个非终结符N连同相应的产生式对应一个语法图

• 小写字母表示终结符
• 大写字母表示非终结符
• 希腊字母表示终结符或非终结符
• 终结符在语法图中表示为圆圈
• 非终结符在语法图中表示为方框

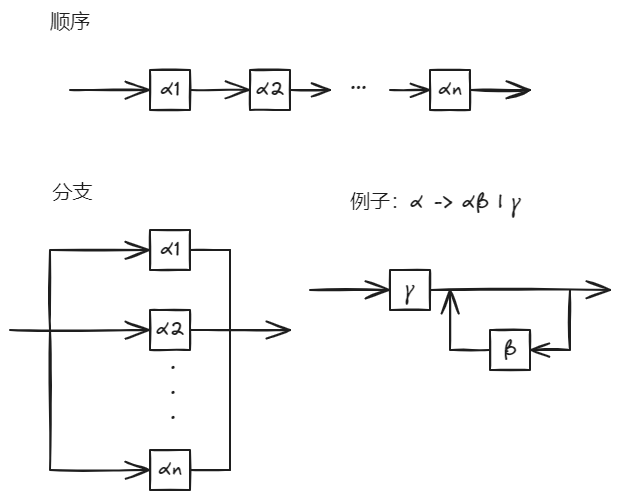
标识符语法图：

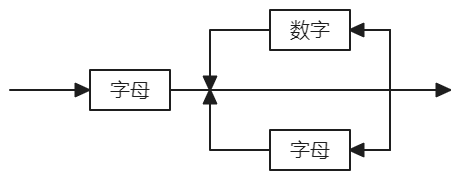
表达式语法图：

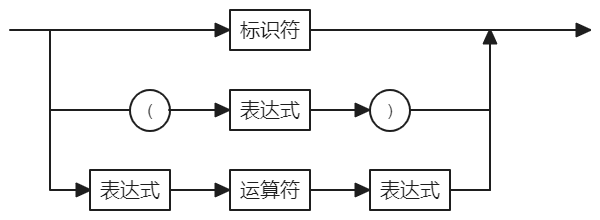
若一个终结符序列是合法的，那么必须从语法图的入口边通过语法图而到达出口边，而且在通过的过程中恰恰能识别该终结符序列。

2. 语义

用以规定语法正确的成分或其成分的含义的一组规则集合。（用以规定程序或其成分的含义的规则）

语言的语义定义语言合法句子的含义，即句子的作用和意义。

GAM抽象机

二、文法

1. 文法的分类

0型文法

• 产生式形如$\alpha\rightarrow\beta$，$\alpha\in V^*V_NV^*$，$\beta\in V^*$
• 又称为短语结构文法
• 0型文法产生的语言称为0型语言
• 0型文法的能力相当于图灵机，递归可枚举

Tips

0型文法唯一的要求是产生式左部要有$V_N$

1型文法

• 产生式形如$\alpha\rightarrow\beta$，$|\alpha|\leq|\beta|$
• $S\rightarrow\varepsilon$除外，S不得出现在任何产生式右部
• 又称为上下文相关文法
• 产生的语言称为1型语言，也称为上下文相关语言
• 生成的语言一定是递归集，递归集不一定是1型语言

Tips

1型语言要求产生式左部个数比右部少

2型文法

• 产生式形如$A\rightarrow\beta$，$A\in V_N$，$\beta\in V^*$
• 又称为上下文无关文法
• 2型文法产生的语言称为2型语言，也称为上下文无关语言（CFL）
• 2型文法的能力相当于下推自动机
• 通常强制式语言属于2型文法

Tips

2型文法要求左部只有1个$V_N$

3型文法

• 产生式形如$A\rightarrow\alpha B$或$A\rightarrow\alpha$，其中$A,B\in V_N$，$\alpha\in V_T^*$
• 又称为正则文法（右线性文法）
• 3型文法产生的语言称为3型语言，也称为正则语言（正则集）
• 3型文法的能力相当于有限自动机
• 3型文法是2型文法的一个子集

Tips

3型文法在2型文法的基础上，右部只有末尾可以有非终结符

2. 文法产生的语言

推导与归约

已知$G(E)=\{E\to E+E|E*E|(E)|i\}$，$i+i*i$的推导过程如下：

E=>E+E=>E+E*E=>E+E*i=>E+i*i=>i+i*i     # 最右推导（规范推导），其逆过程为最左归约（规范归约）
E=>E+E=>i+E=>i+E*E=>i+i*E=>i+i*i       # 最左推导，逆过程最右归约

一些概念

设文法$G=(V_T,V_N,S,P)$，$\alpha,\beta\in V^*$

1. 如果$S{\overset{*}{\Rightarrow}}\alpha$，$\alpha\in V^*$，则$\alpha$为G的一个句型

Tips

语法树生长过程中的任何时刻，所有那些没有后代的末端结点的标记自左向右的排列就是一个句型。

2. 如果$S{\overset{*}{\Rightarrow}}\alpha$，$\alpha\in V_T^*$，则$\alpha$为G的一个句子
3. 文法G的所有句子的集合称为G产生的语言，记为L(G)，即：$L(G)=\{\alpha|S{\overset{*}{\Rightarrow}}\alpha,\alpha\in V_T^*\}$

Note

文法$G=\{S\to aS|b\}$产生的语言$L(G)=\{a^nb|n\geq0\}$

语法树

语法树（推导树）是一棵用来表示一个句型的推导过程的树，它满足

• 每个结点带有一个唯一的标记，标记是文法G的非终结符或终结符
• 如果标记为非终结符A的内部结点从左到右有子节点$X_1,X_2,\ldots,X_n$，则$A\to X_1\ldots X_n$是一个产生式

例：$G(E)=\{E\to E+E|E*E|(E)|i\}$，句子$i+i*i$的语法树如下图：

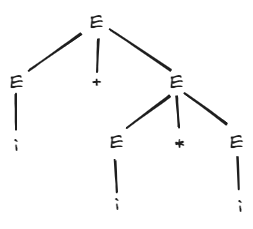
Caution

$i+i*i$还存在不同的语法树

如果一个文法存在某个句子有多于一个的语法树，则称这个文法是二义文法

几个结论：

• 一个二义文法产生的语言不一定是二义语言
• 二义性的问题是不可判定的
• 存在先天二义语言；即，每个产生它的文法都是二义的

三、一些设计准则

• 可写性（简单性、可表达性、正交性、准确性）
• 可读性
• 可靠性