Appearance
第七章 自上而下的语法分析
自上而下的语法分析:从开始符号S出发,看能否找到一个最右推导,使得;或从S出发,能否构成一个语法树,使得树的叶节点自左向右构成。
一、回溯分析法
1. 提取公共左因子
提取公共左因子后:
2. 消除左递归
消除直接左递归
直接左递归:文法中直接出现左递归,即有形如的产生式。
产生无限推导。
将左递归的产生式改写成等价的右递归的产生式。
改写后:
消除间接左递归
间接左递归:通过推导产生的左递归。
存在间接左递归同样会产生无限推导。
例:
- 用R代入Q
- 用Q代入S
消除直接左递归:
- Q和R为多余可删除,最后答案如上式
二、递归下降分析法
当文法改造为无公共左因子,无左递归时,让每个非终结符对应一个过程,该过程对相应的非终结符产生式的右部短语进行语法分析。
文法,消除左递归后得到:
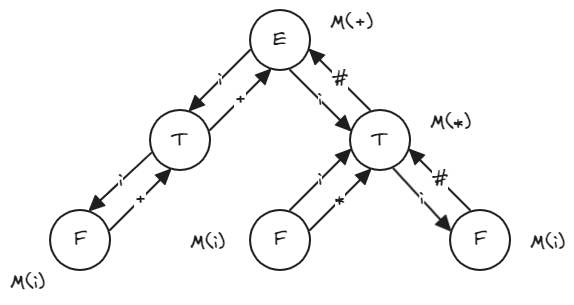
对输出串的执行过程:
扩充的BNF
- 表示的0到任意多次重复,即
- 表示0次到n次重复,
- 表示可有可无(即)
文法G可以改写为:
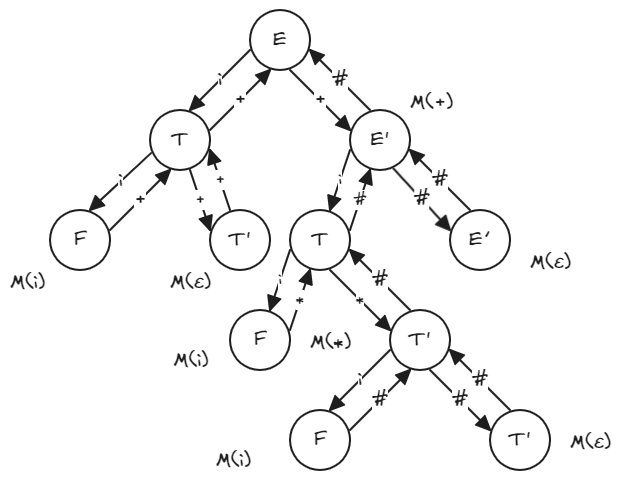
的分析过程:
三、预测分析法
是一种表驱动方法,由下推栈、预测分析表和控制程序组成,它实际上是一种下推自动机的实现模型。
预测分析表
- 形式:矩阵,,
- 内容:或出错标志(空白)
例:文法,消除左递归后得到
1. 构造FIRST集和FOLLOW集
FIRST集:
- ,
- ,
- ,可产生,
FOLLOW集:
- ,
- ,
- ,
- ,可以产生,
| FIRST | FOLLOW | |
|---|---|---|
| E | ( i | ) # |
| E' | + ε | ) # |
| T | ( i | + ) # |
| T' | * ε | + ) # |
| F | ( i | * + ) # |
2. 构造预测分析表
- 横与,纵
- ,填对应产生式
- 可以产生,,填
| i | * | + | ( | ) | # | |
|---|---|---|---|---|---|---|
| E | E->TE' | E->TE' | ||||
| E' | E'->+TE' | E'->ε | E'->ε | |||
| T | T->FT' | T->FT' | ||||
| T' | T'->*FT' | T'->ε | T'->ε | T'->ε | ||
| F | F->i | F->(E) |
3. 预测分析过程
- 栈、输入串、归约
- 栈放
- 根据栈顶与当前字符查表归约,产生式右部倒序入栈
| 栈 | 输入串 | 归约 |
|---|---|---|
| #E | i+i*i# | E->TE' |
| #E'T | i+i*i# | T->FT' |
| #E'T'F | i+i*i# | F->i |
| #E'T' | +i*i# | T'->ε |
| #E' | +i*i# | E'->+TE' |
| #E'T | i*i# | T->FT' |
| #E'T'F | i*i# | F->i |
| #E'T' | *i# | T'->*FT' |
| #E'T'F | i# | F->i |
| #E'T' | # | T'->ε |
| #E' | # | E'->ε |
| # | # | acc |
4. LL(1)文法
设有文法,若它的任一产生式,均满足:
- ,其中,
- 若,则,且
则文法G称为LL(1)文法。
自上而下分析时,若当前输入字符为,分析栈待匹配的非终结符为A,,则当
- 若,
则便是唯一与匹配的产生式。即LL(1)文法中的两个条件保证了自上而下匹配的唯一性。
Note
预测分析表没有多重入口,则该文法是LL(1)文法。

