一、自下而上的语法分析

自下而上的语法分析：从$\omega$开始，看能否找到一个规范归约，逐步向上归约，直到开始符号S。

设有文法

$$\begin{aligned} S\to &SAS\\ S\to &b\\ A\to &ccA\\ A\to &a \end{aligned}$$

输入串$bccab$的归约过程：

栈	输入串	归约
	bccab
b	ccab	S->b
S	ccab
Scca	b	A->a
SccA	b	A->ccA
SA	b
SAb		S->b
SAS		S->SAS
S

分析树的生成（裁剪）过程：

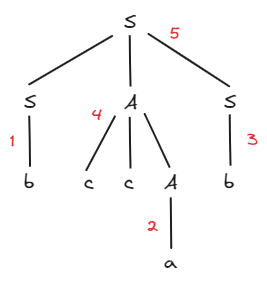
二、几个核心概念

短语

设有文法$G$，$S$是开始符号，设$\alpha\beta\delta$是$G$的一个句型，若有$S{\overset{+}{\Rightarrow}}\alpha A\delta$且$A{\overset{+}{\Rightarrow}}\beta$，则称$\beta$是句型$\alpha\beta\delta$关于$A$的短语。

直接短语

在上面的定义中，如果$A$直接推出$\beta$，即$A\Rightarrow \beta$，则称$\beta$是句型$\alpha\beta\delta$关于$A\to\beta$的直接短语。

句柄

一个句型的最左直接短语称为句柄。

例

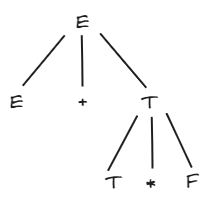
• 短语：T*F、E+T*F
• 直接短语：T*F
• 句柄：T*F

三、算符优先文法

Note

适合于表达式的分析。

不严格按照最左归约进行，不是规范归约。

以文法$G$为例：

$$\begin{aligned} E\to &E+T|T\\ T\to &T*F|F\\ F\to &(E)|i \end{aligned}$$

1. 基本概念

算符文法

如果一个文法的任何产生式都不含两个或两个以上的相连的非终结符，且不含$\varepsilon$产生式，则称该文法为算符文法。

算符之间的优先关系

对算符文法$G$，$a,b\in V_T$，$P,Q\in V_N$，定义：

• $a=b$：$G$中有$P\to\ldots ab\ldots$或$P\to\ldots aQb\ldots$
• $a<b$：$G$中有$P\to\ldots aQ\ldots$且$Q\overset{+}{\Rightarrow}b\ldots$或$Q\overset{+}{\Rightarrow}Rb\ldots$
• $a>b$：$G$中有$P\to\ldots Qb\ldots$且$Q\overset{+}{\Rightarrow}\ldots a$或$Q\overset{+}{\Rightarrow}\ldots aR$

算符优先文法

如果算符优先文法$G$的任何两个终结符之间的关系至多只有<，=，>中的一个优先关系，则称该文法为算符优先文法。

Warning

优先关系表中没有多重入口，即为算符优先文法。

优先关系表

记录一个文法$G$中所有非终结符之间的优先关系。

Note

优先关系不是数学关系：a<b未必有b>a，终结符之间未必有优先关系，优先关系不能传递。

素短语

素短语：文法$G$某句型的一个短语$\alpha$是素短语，当且仅当它至少含有一个终结符，且除它自身外不再含更小的素短语。

最左素短语：在具有多个素短语的句型中处于最左边的那个素短语。

• 素短语：T*F
• 最左素短语：T*F

2. 构造FIRSTVT集和LASTVT集

FIRSTVT集：非终结符能推出的第一个终结符的集合

• $P\to a\ldots$或$P\to Qa\ldots$，则$a\in FIRSTVT(P)$
• $P\to Q\ldots$，则$FIRSTVT(Q)\subset FIRSTVT(P)$

LASTVT集：非终结符能推出的最后一个终结符的集合

• $P\to\ldots a$或$P\to\ldots aQ$，则$a\in LASTVT(P)$
• $P\to\ldots Q$，则$LASTVT(Q)\subset LASTVT(P)$

	FIRSTVT	LASTVT
E	+ * ( i	+ * ) i
T	* ( i	* ) i
F	( i	) i

3. 构造优先关系表

• 横竖都是$V_T$与$\#$
• 增加产生式$S'\to\#S\#$
• $P\to\ldots aQ\ldots$，则$a<FIRSTVT(Q)$（即$a$行横填<）
• $P\to\ldots Qa\ldots$，则$a>LASTVT(Q)$（即$a$列纵填>）

	i	+	*	(	)	#
i		>	>		>	>
+	<	>	<	<	>	>
*	<	>	>	<	>	>
(	<	<	<	<	=
)		>	>		>	>
#	<	<	<	<		=

4. 算符优先分析过程

• 栈、输入串、动作
• 栈放$\#$
• $[\text{最靠近栈顶的}V_T,\text{当前字符}]$查表
• $\#=\#$，acc

栈	输入串	动作
#	i+i*i#	#<i，移进
#i	+i*i#	i>+，归约，F->i
#F	+i*i#	#<+，移进
#F+	i*i#	+<i，移进
#F+i	*i#	i>*，归约，F->i
#F+F	*i#	+<*，移进
#F+F*	i#	*<i，移进
#F+F*i	#	i>#，归约，F->i
#F+F*F	#	*>#，归约，T->T*F
#F+T	#	+>#，归约，E->E+T
#E	#	#=#，acc

四、LR分析法

1. LR分析法的种类

• LR(0)分析法
• SLR分析法
• 规范LR分析法
• LALR分析法

2. 几个概念

活前缀

规范句型中不含句柄之后任何一个符号的一个前缀。

如：$S\overset{*}{\Rightarrow}\delta A\omega\overset{*}{\Rightarrow}\delta\alpha\beta\omega$，$\delta\alpha\beta$及其任何前缀都是$\delta\alpha\beta\omega$的活前缀

Note

$\alpha\beta$是句柄，$\alpha\beta$及前任何前缀均不包含句柄之后的符号，而$\alpha\beta$是$\delta\alpha\beta$的后缀，是分析栈栈顶符号串。

规范归约的特点

• 归约符号串总是在栈顶
• 句柄之后的待入栈符号串总是终结符
• 规范句型（由规范推导推出的句型）在符号栈中的符号串是规范句型的前缀

活前缀与句柄之间的关系

• 归约符号串总是在栈顶
• 句柄之后的待入栈符号串总是终结符
• 规范句型（由规范推导推出的句型）在符号栈中的符号串是规范句型的前缀

活前缀与句柄之间的关系

• 活前缀不含句柄的任何符号，$A\to\cdot\alpha\beta$
• 活前缀只含句柄的真前缀，$A\to\alpha\cdot\beta$
• 活前缀包含句柄的全部符号，$A\to\alpha\beta\cdot$

LR(0)项目

在一个产生式右部添加一个圆点，称为一个LR(0)项目。

Note

圆点左边已识别，右边期待识别。

LR(0)项目的分类

• 归约项目：形如$A\to\alpha\cdot$
• 移进项目：形如$A\to\alpha\cdot a\beta$，$a\in V_T$
• 待约项目：形如$A\to\alpha\cdot B\beta$，$B\in V_N$
• 接受项目：形如$S\to\alpha\cdot$，$S$为开始符号

文法的拓广

在文法$G$中增加产生式$S'\to S$，从而使$S'\to S\cdot$成为唯一的接受项目。

3. 构造识别所有活前缀的转换图

• 每个状态是一个LR(0)项目
• $S'\to\cdot S$是唯一初态
• $X\to\ldots X_{i-1}\cdot X_i\ldots\overset{X_i}{\Rightarrow}X\to\ldots X_{i-1}X_i\cdot\ldots$
• 如果上一条规则的$X_i$是$V_N$，$X\to X_{i-1}\cdot X_i\overset{\varepsilon}{\Rightarrow}X_i\to\alpha_1|\alpha_2|\ldots|\alpha_m$

例：$G=\{S\to BB,B\to aB|b\}$

1. $S'\to\cdot S$
2. $S'\to S\cdot$
3. $S\to\cdot BB$
4. $S\to B\cdot B$
5. $S\to BB\cdot$
6. $B\to\cdot aB$
7. $B\to a\cdot B$
8. $B\to aB\cdot$
9. $B\to\cdot b$
10. $B\to b\cdot$

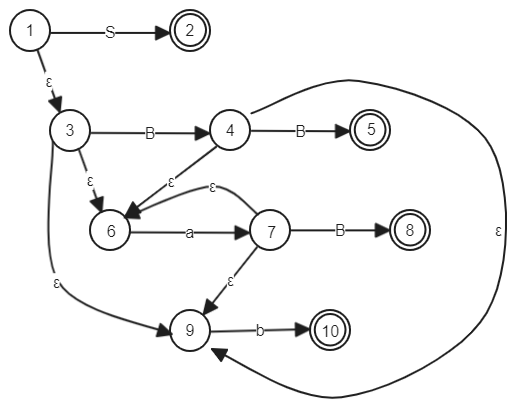
4. 构造LR(0)项目集规范族

• 有效项目：对于项目$A\to\alpha\cdot\beta$，如果有$S\overset{*}{\Rightarrow}\delta A\omega\Rightarrow\delta\alpha\beta\omega$，则称$A\to\alpha\cdot\beta$对活前缀$\delta\alpha$有效
• 有效项目集：对于一个活前缀有效的项目可能不止一个，对活前缀$\delta\alpha$有效的项目集合称为$\delta\alpha$的有效项目集
• LR(0)项目集规范族：文法$G$的所有有效项目集组成的集合

写出上例的LR(0)项目集规范族

I0=closure{S'->.S}={S'->.S,S->.BB,B->.aB,B->.b}
I1=go(I0,S)={S'->S.}
I2=go(I0,B)={S->B.B,B->.aB,B->.b}
I3=go(I0,a)=go(I2,a)=go(I3,a)={B->a.B,B->.aB,B->.b}
I4=go(I0,b)=go(I2,b)=go(I3,b)={B->b.}
I5=go(I2,B)={S->BB.}
I6=go(I3,B)={B->aB.}

5. 构造LR(0)分析表

有多少状态就有多少行，action表头$V_T$与$\#$，goto表头$V_N$

• 接收项：$action[k,\#]=acc$
• 移进项：$go(I_k,a)=I_j$，$action[k,a]=s_j$
• $I_k$中的归约项，$A\to\alpha$为第$j$个产生式，$action[k,\text{所有非终结符或}\#]=r_j$
• $go(I_k,A)=I_j$，$goto[k,A]=j$
• 空白：错误

接上例：

	a	b	#	S	B
0	s3	s4
1			acc	1	2
2	s3	s4
3	s3	s4			5
4	r3	r3	r3		6
5	r1	r1	r1
6	r2	r2	r2

Warning

LR(0)分析表中没有多重入口说明是LL(1)文法

6. 构造SLR(1)分表

构造$V_N$的FOLLOW集，产生式左部$V_N$的FOLLOW集中的$V_T$才填$r_j$

接上例：

	FIRST	FOLLOW
S	a b	a b #
B	a b	a b #

	a	b	#	S	B
0	s3	s4		1	2
1			acc
2	s3	s4			5
3	s3	s4			6
4	r3	r3	r3
5	r1	r1	r1
6	r2	r2	r2

Warning

SLR(1)分析表中没有多重入口说明是SLR(1)文法

7. 分析过程

action表与goto表

action表：$action[S,a]$定义了在状态S下，当输入字符为a时应采取的动作

• $s_j$：j入状态栈，输入指针所指符号入符号栈
• $r_j$：按第j个产生式归约，状态栈出栈产生式右部符号个数，左部入符号栈，goto后的状态入状态栈
• acc：成功
• 空白：出错

goto表：$goto[S,x]$定义了在状态S下，面对文法符号x时状态的转换

分析步骤

• 状态栈、符号栈、输入串、动作
• 状态栈放0，符号栈放#
• $action[\text{状态栈顶},\text{当前字符}]$
  • $s_j$：j入状态栈，当前字符入符号栈
  • $r_j$：根据第j个产生式归约，两个栈都出栈右部个数。左部入符号栈，$goto[\text{状态栈顶},\text{产生式左部}]$入状态栈

接上例，输入串aabb的分析过程如下：

状态	符号	输入串	动作
0	#	aabb#	s3
03	#a	aabb#	s3
033	#aa	bb#	s4
0334	#aab	b#	r3，B->b，goto[3,B]
0336	#aaB	b#	r2，B->aB，goto[3,B]
036	#aB	b#	r2，B->aB，goto[0,B]
02	#B	b#	s4
024	#Bb	#	r3，B->b，goto[2,B]
025	#BB	#	r1，S->BB，goto[0,S]
01	#S	#	acc