一、死锁

1. 产生死锁的原因

1. 竞争资源

   • 可剥夺和非剥夺性资源
   • 竞争非剥夺性资源
   • 竞争临时性资源

2. 进程间推进顺序不当

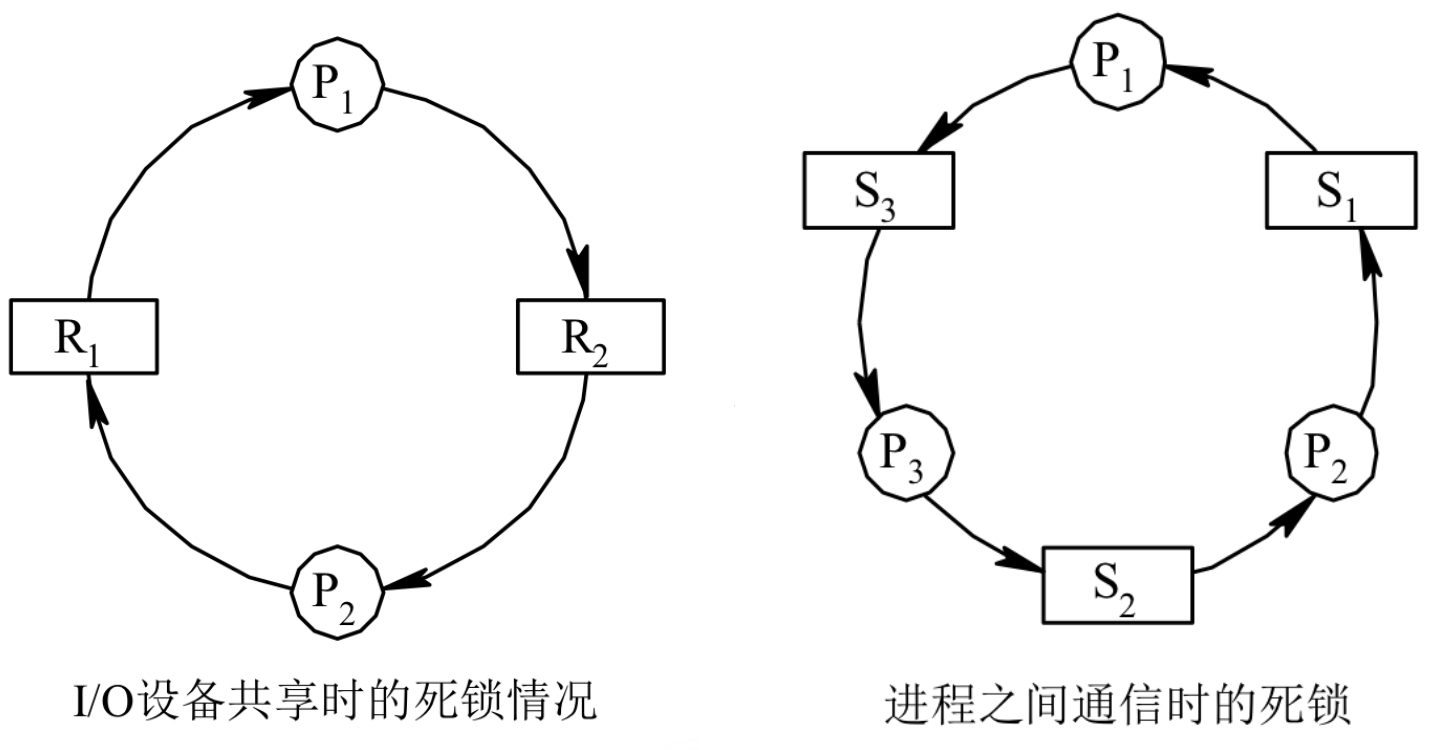
2. 产生死锁的必要原因

• 互斥条件

• 请求和保持条件

• 不可抢占条件

• 环路等待条件

3. 处理死锁的基本方法

• 预防死锁

• 避免死锁

• 检测死锁

• 接触死锁

二、预防死锁

破坏死锁发生的可能

1. 摒弃“请求和保持”条件要求进程在执行前，一次申请完它在执行过程中可能会用到的所有资源

2. 摒弃“不剥夺”条件

   • 如果进程占用了一些资源，且后续的资源请求得不到满足，它必须释放已经占用的资源，并在后续的执行中一次申请其需要的所有资源
   • 一个高优先级进程申请已经被低优先级进程占用的资源，os将从后者处抢占资源分配给前者，此方法仅用于资源状态容易保存与恢复的场合

3. 摒弃“环路等待”条件使用有序资源分配法，首先将资源进行排序，如果进程获得资源R，则它后续请求的资源序号只能都大于或者都小于R

安全状态

在避免死锁的方法中，允许进程动态地申请资源，但系统在进行资源分配之前，应先计算此次资源分配的安全性。

若此次分配不会导致系统进入不安全状态，则将资源分配给进程；否则，令进程等待。

所谓安全状态，是指系统能按某种进程顺序(P1, P2, …, Pn)(称〈P1, P2, …, Pn〉序列为安全序列)，来为每个进程Pi分配其所需资源，直至满足每个进程对资源的最大需求，使每个进程都可顺利地完成。如果系统无法找到这样一个安全序列，则称系统处于不安全状态。

举例

我们通过一个例子来说明安全性。假定系统中有三个进程P1、P2和P3，共有12台磁带机。进程P1总共要求10台磁带机，P2和P3分别要求4台和9台。假设在T0时刻，进程P1、P2和P3已分别获得5台、2台和2台磁带机，尚有3台空闲未分配，如下表所示：

进程	最大需求	已分配	可用
P1	10	5	3
P2	4	2
P3	9	2

由安全状态向不安全状态的转换

如果不按照安全序列分配资源，则系统可能会由安全状态进入不安全状态。例如，在T0时刻以后，P3又请求1台磁带机，若此时系统把剩余3台中的1台分配给P3，则系统便进入不安全状态。因为，此时也无法再找到一个安全序列，例如，把其余的2台分配给P2，这样，在P2完成后只能释放出4台，既不能满足P1尚需5台的要求，也不能满足P3尚需6台的要求，致使它们都无法推进到完成，彼此都在等待对方释放资源，即陷入僵局，结果导致死锁。

三、避免死锁

利用银行家算法避免死锁

1. 银行家算法中的数据结构

可利用资源向量Available

这是一个含有$m$个元素的数组，其中的每一个元素代表一类可利用的资源数目，其初始值是系统中所配置的该类全部可用资源的数目，其数值随该类资源的分配和回收而动态地改变。如果Available[j]==K，则表示系统中现有$R_j$类资源$K$个。

最大需求矩阵Max

这是一个$n\times m$的矩阵，它定义了系统中$n$个进程中的每一个进程对$m$类资源的最大需求。如果Max[i,j]==K，则表示进程$i$需要$R_j$类资源的最大数目为$K$。

分配矩阵Allocation

这也是一个$n\times m$的矩阵，它定义了系统中每一类资源当前已分配给每一进程的资源数。如果Allocation[i,j]==K，则表示进程$i$当前已分得$R_j$类资源的数目为$K$。

需求矩阵Need

这也是一个$n\times m$的矩阵，用以表示每一个进程尚需的各类资源数。如果Need[i,j]==K，则表示进程$i$还需要$R_j$类资源$K$个，方能完成其任务。

Need[i,j]=Max[i,j]-Allocation[i,j]

2. 银行家算法

设$Request_i$是进程$P_i$的请求向量，如果Requesti[j]==K，表示进程$P_i$需要$K$个$R_j$类型的资源。当$P_i$发出资源请求后，系统按下述步骤进行检查：

1. 如果Request_i[j]<=Need[i,j]，便转向步骤2；否则认为出错，因为它所需要的资源数已超过它所宣布的最大值。

2. 如果Request_i[j]<=Available[j]，便转向步骤(3)；否则，表示尚无足够资源，$P_i$须等待。

3. 系统试探着把资源分配给进程$P_i$，并修改下面数据结构中的数值：

Available[j]∶=Available[j]-Requesti[j];
Allocation[i,j]∶=Allocation[i,j]+Requesti[j];
Need[i,j]∶=Need[i,j]-Requesti[j];

4. 系统执行安全性算法，检查此次资源分配后，系统是否处于安全状态。若安全，才正式将资源分配给进程$P_i$，以完成本次分配；否则，将本次的试探分配作废，恢复原来的资源分配状态，让进程$P_i$等待。

3. 安全性算法

1. 设置两个向量

   1. 工作向量Work：它表示系统可提供给进程继续运行所需的各类资源数目，它含有$m$个元素，在执行安全算法开始时，Work∶=Available;

   2. Finish：它表示系统是否有足够的资源分配给进程，使之运行完成。开始时先做Finish[i]∶=false;当有足够资源分配给进程时，再令Finish[i]∶=true;

2. 从进程集合中找到一个能满足下述条件的进程：

   1. Finish[i]==false;

   2. Need[i,j]<=Work[j];若找到，执行步骤3，否则，执行步骤4。

3. 当进程$P_i$获得资源后，可顺利执行，直至完成，并释放出分配给它的资源，故应执行：

Work[j]∶=Work[i]+Allocation[i,j];
Finish[i]∶=true;
go to step 2;

4. 如果所有进程的Finish[i]==true都满足，则表示系统处于安全状态；否则，系统处于不安全状态。

4. 银行家算法例

假定系统中有五个进程$\{P_0, P_1, P_2, P_3, P4\}$和三类资源${A, B, C}$，各种资源的数量分别为10、5、7，在$T_0$时刻的资源分配情况如图所示。

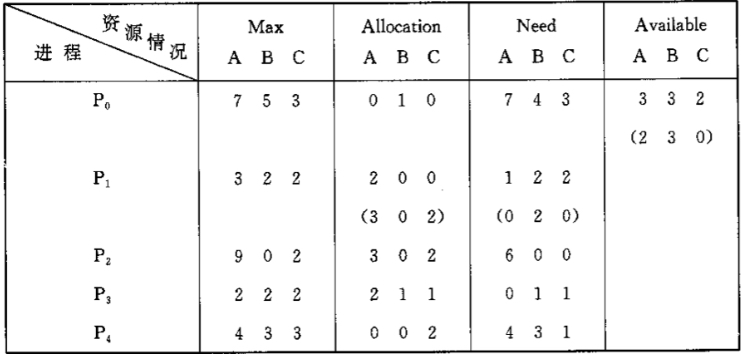
1. $T_0$时刻的安全性

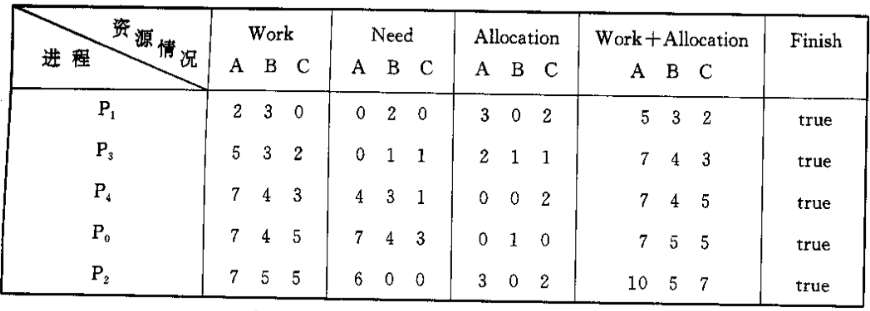
2. $P_1$请求资源：$P_1$发出请求向量Request_1(1,0,2)，系统按银行家算法进行检查：

   1. Request_1(1, 0, 2)<=Need_1(1, 2, 2)
   2. Request_1(1, 0, 2)<=Available_1(3, 3, 2)
   3. 系统先假定可为$P_1$分配资源，并修改Available，Allocation_1和Need_1向量，由此形成的资源变化情况如例图中的圆括号所示。
   4. 再利用安全性算法检查此时系统是否安全。

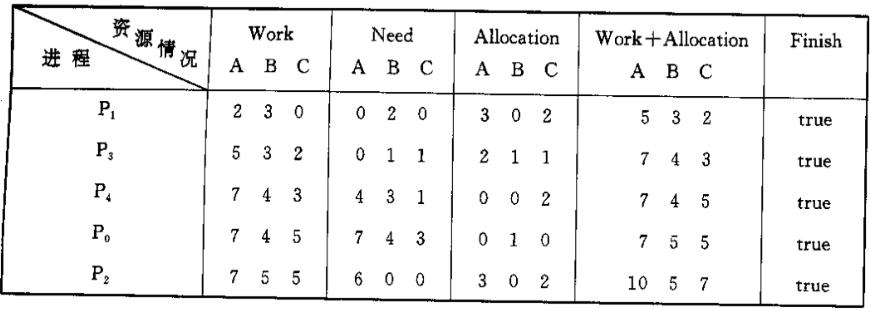
3. $P_4$请求资源：$P_4$发出请求向量Request_4(3,3,0)，系统按银行家算法进行检查：

   1. Request_4(3, 3, 0)<=Need_4(4, 3, 1)
   2. Request_4(3, 3, 0)<Available(2, 3, 0)，让$P_4$等待。

4. $P_0$请求资源：$P_0$发出请求向量Requst_0(0,2,0)，系统按银行家算法进行检查：

   1. Request_0(0, 2, 0)<=Need_0(7, 4, 3)
   2. Request_0(0, 2, 0)<=Available(2, 3, 0)
   3. 系统暂时先假定可为$P_0$分配资源，并修改有关数据，如图所示。

四、检测死锁

1. 资源分配图

每类资源有多个时的情况

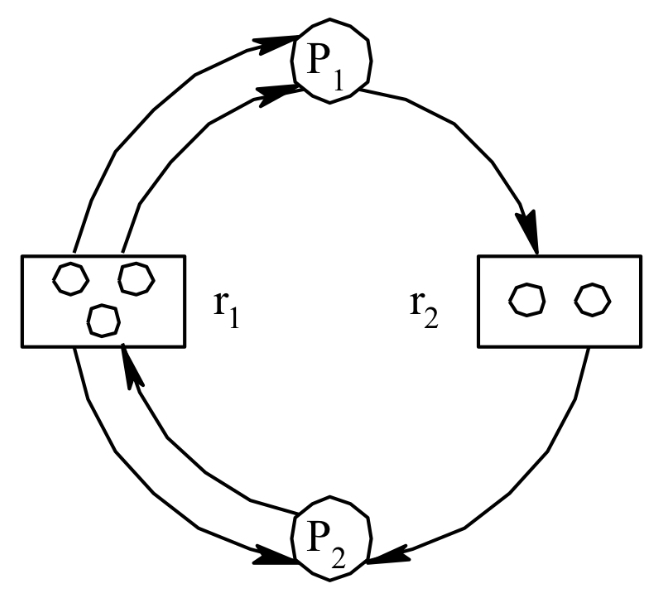
凡属于$E$中的一个边$e\in E$，都连接着P中的一个结点和R中的一个结点，$e=\{p_i,r_j\}$是资源请求边，由进程$p_i$指向资源$r_j$，它表示进程$p_i$请求一个单位的$r_j$资源。$e=\{r_j,p_i\}$是资源分配边，由资源$r_j$指向进程$p_i$，它表示把一个单位的资源$r_j$分配给进程$p_i$。

2. 死锁定理

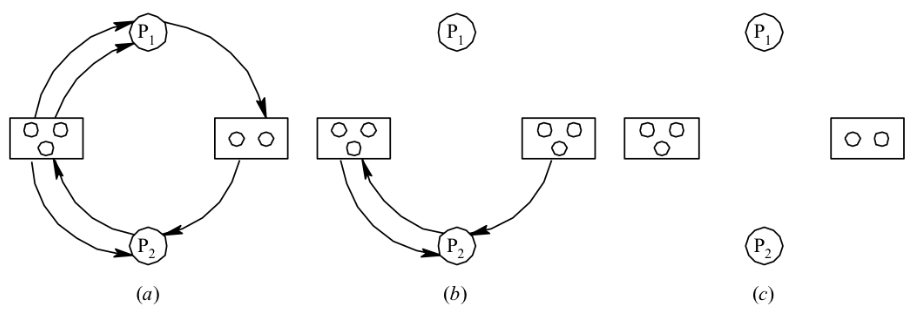
资源分配图的简化

3. 死锁检测中的数据结构

1. 可利用资源向量Available，它表示了$m$类资源中每一类资源的可用数目。

2. 把不占用资源的进程(向量Allocation∶=0)记入L表中，即$L_i\cup L$。

3. 从进程集合中找到一个Request_i<=Work的进程，做如下处理：

   1. 将其资源分配图简化，释放出资源，增加工作向量Work∶=Work+Allocation_i。
   2. 将它记入L表中。

4. 若不能把所有进程都记入L表中，便表明系统状态S的资源分配图是不可完全简化的。因此，该系统状态将发生死锁。

五、解除死锁

• 剥夺资源

• 撤消进程

为把系统从死锁状态中解脱出来，所花费的代价可表示为：

$R(S)_{min}=min\{C_{ui}\}+min\{C_{uj}\}+min\{C_{uk}\}+\ldots$