问题：

• 穷举法在维度高区间大的情况下会导致庞大的计算量
• 分治法可能会陷入局部最优，维度高划分空间也会导致庞大的计算量

优化问题（Optimization Problem）：在给定约束条件下，找到一个目标函数的最优解（最大值或最小值）。

$$\omega^*=\mathop{\arg\min}\limits_{\omega}\ cost(\omega)$$

解决优化问题使用梯度下降算法（Gradient Descent Algorithm）。

梯度的定义：

$$Gradient=\frac{\partial cost}{\partial\omega}$$

更新权重的方法：

$$\omega=\omega-\alpha\frac{\partial cost}{\partial\omega}$$

$\alpha$是学习率，会影响更新的步长（一般设置得较小），负号表示向梯度负方向更新权重。

每一次更新都是作出当下最好的选择，所以梯度下降算法是一种贪心算法，不一定能够得到全局最优解。

依旧使用梯度下降算法的原因是，深度神经网络的损失函数中局部最优点不多，但是存在鞍点导致$\omega$无法继续迭代。

算法步骤：

1. Initial Guess: $\omega$
2. 计算该点的梯度
3. 更新$\omega$
4. 重复2和3直到找到极值（局部最优）

继续上一节：

$$\begin{aligned} \frac{\partial cost(\omega)}{\omega}&=\frac{\partial}{\partial\omega}\frac{1}{N}\sum_{n=1}^N(x_n\cdot\omega-y_n)^2\\ &=\frac{1}{N}\sum_{n=1}^N\frac{\partial}{\partial\omega}(x_n\cdot\omega-y_n)^2\\ &=\frac{1}{N}\sum_{n=1}^N2\cdot(x_n\cdot\omega-y_n)\frac{\partial(x_n\cdot\omega-y_n)}{\partial\omega}\\ &=\frac{1}{N}\sum_{n=1}^N2\cdot x_n\cdot(x_n\cdot\omega-y_n) \end{aligned}$$

Update:

$$\omega=\omega-\alpha\frac{1}{N}\sum_{n=1}^N2\cdot x_n\cdot(x_n\cdot\omega-y_n)$$

代码：

import matplotlib.pyplot as plt  
  
# 训练集  
x_data = [1.0, 2.0, 3.0]  
y_data = [2.0, 4.0, 6.0]  
  
# initial guess  
w = 1.0  
  
  
# 计算y_pred  
def forward(x): return x*w  
  
  
# 计算损失  
def cost(xs, ys):  
    cost = 0  
    for x, y in zip(xs, ys):  
        y_pred = forward(x)  
        cost += (y_pred-y) ** 2  
    return cost / len(xs)  
  
  
# 计算梯度  
def gradient(xs, ys):  
    grad = 0  
    for x, y in zip(xs, ys):  
        grad += 2 * x * (x * w - y)  
    return grad / len(xs)  
  
  
cost_list = []  
epoch_list = []  
  
# 训练过程  
print('Predict (before training)', 4, forward(4))  
for epoch in range(100):                 # 训练100轮  
    cost_val = cost(x_data, y_data)      # 求损失  
    grad_val = gradient(x_data, y_data)  # 求梯度  
    w -= 0.01 * grad_val                 # 更新，学习率为0.01  
    cost_list.append(cost_val)  
    epoch_list.append(epoch)  
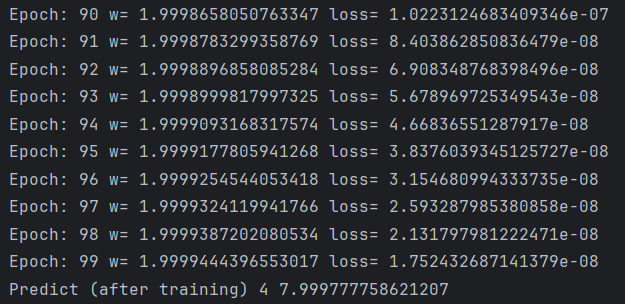
    print('Epoch:', epoch, 'w=', w, 'loss=', cost_val)  
print('Predict (after training)', 4, forward(4))  
  
# 可视化  
plt.plot(epoch_list, cost_list)  
plt.ylabel('Cost')  
plt.xlabel('Epoch')  
plt.show()

运行结果：

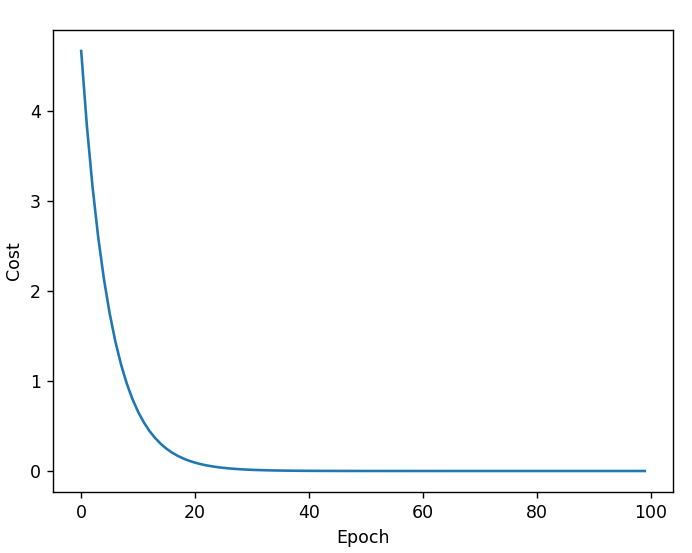
如果能够收敛，那么epoch-cost的关系一般如上图所示，在前几轮cost会下降得非常快，然后越来越慢。如果是发散的那么本次训练失败，可以考虑取较低的学习率。

在实际训练中，曲线并不会如此平滑，甚至可能出现较大的波动，所以绘图时可以采用指数加权均值的cost以获得较为平滑的曲线。

$$\begin{aligned} cost_0' &=cost_0\\ cost_i' &=\beta cost_i+(1-\beta)cost_{i-1}' \end{aligned}$$

具体应用一般不采用梯度下降（Gradient Descent），而是采用随机梯度下降（Stochastic Gradient Descent）。

Stochastic Gradient Descent更新权重的方式：

$$\omega=\omega-\alpha\frac{\partial loss}{\partial\omega}$$

为什么使用loss而不使用cost？因为，cost是全部loss的平均，而loss是单个样本的可能有随机噪声，使用loss可能可以跨越鞍点。

考虑上节例子，那么

$$\begin{aligned} \frac{\partial loss_n}{\partial\omega}&=\frac{\partial(x_n\cdot\omega-y_n)^2}{\partial\omega}\\ &=2\cdot(x_n\cdot\omega-y_n)\frac{\partial(x_n\cdot\omega-y_n)}{\partial\omega}\\ &=2\cdot x_n\cdot(x_n\cdot\omega-y_n) \end{aligned}$$

代码：

# 训练集  
x_data = [1.0, 2.0, 3.0]  
y_data = [2.0, 4.0, 6.0]  
  
# initial guess  
w = 1.0  
  
  
# 计算y_pred  
def forward(x): return x*w  
  
  
# 计算损失  
def loss(x, y):  
    y_pred = forward(x)  
    return (y_pred - y) ** 2  
  
  
# 计算梯度  
def gradient(x, y):  
    return 2 * x * (x * w - y)  
  
  
# 训练过程  
print('Predict (before training)', 4, forward(4))  
for epoch in range(100):                 # 训练100轮  
    for x, y in zip(x_data, y_data):  
        grad = gradient(x, y)  
        w = w - 0.01*grad  
        print('\tgrad:', x, y, grad)  
        l = loss(x, y)  
    print('progress:', epoch, 'w=', w, 'loss=', l)  
print('Predict (after training)', 4, forward(4))

Warning

梯度下降$f(x_i)$和$f(x_{i+1})$是没有依赖关系的，可以并行。而随机梯度下降的$g(x_i)$和$g(x_{i+1})$是存在依赖关系的，不能利用并行。

梯度下降具有更好的性能，而随机梯度下降具有更好的时间复杂度。实际上会在二者之间取一个折中，即批量的随机梯度下降，把样本分为Mini-Batch，进行随机梯度下降。