Diabetes Dataset

以Diabetes数据集为例，它需要处理多维特征的输入（Multiple Dimension Input）。

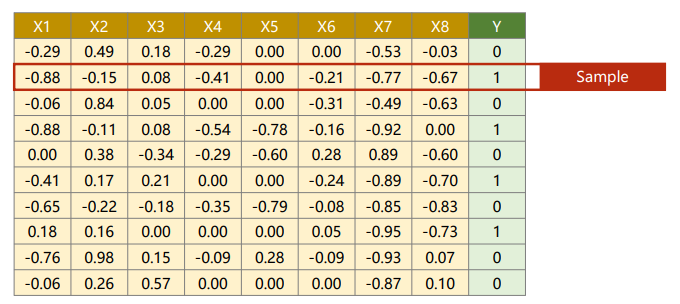
一行称为一个样本（Sample）

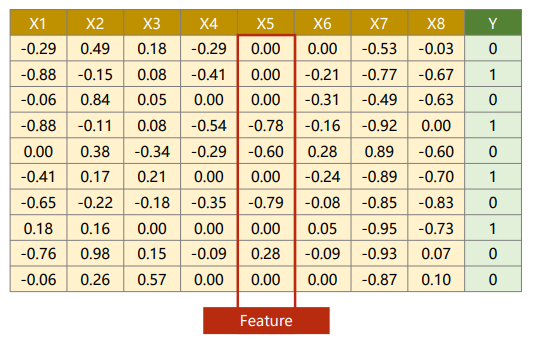
一列称为一个特征（Feature）。

Multiple Dimension Logistic Regression Model

单个特征输入的逻辑斯蒂回归模型：

$$\hat y^{(i)}=\sigma(x^{(i)}\times\omega+b)$$

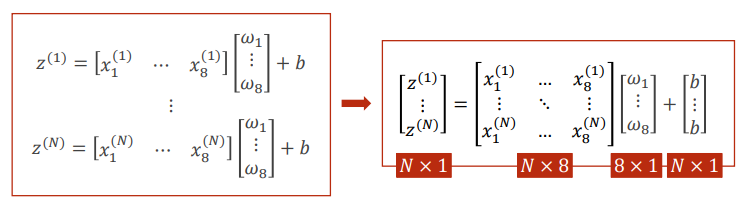
多维特征输入的逻辑斯蒂回归模型：

$$\hat y^{(i)}=\sigma(\sum_{n=1}^8x_n^{(i)}\cdot\omega_n+b)$$

以Diabetes Dataset为例，因为：

$$\sum_{n=1}^8x_n^{(i)}\cdot\omega_n=[x_1^{(i)}\cdots x_8^{(i)}]\left [\begin{array}{c} \omega_1\\ \vdots\\ \omega_8 \end{array}\right]$$

所以多维特征输入的逻辑斯蒂回归模型可以写为：

$$\begin{align*} \hat y^{(i)}&=\sigma([x_1^{(i)}\cdots x_8^{(i)}]\left [\begin{array}{c} \omega_1\\ \vdots\\ \omega_8 \end{array}\right]+b)\\ &=\sigma(z^{(i)}) \end{align*}$$

Mini-Batch(N samples)

Sigmoid function is in an element-wise fashion.

$$\left [\begin{array}{c} \hat y^{(1)}\\ \vdots\\ \hat y^{(N)} \end{array}\right]=\left [\begin{array}{c} \sigma(z^{(1)})\\ \vdots\\ \sigma(z^{(N)}) \end{array}\right]=\sigma( \left [\begin{array}{c} z^{(1)}\\ \vdots\\ z^{(N)} \end{array}\right])$$

Tips

将数据转化为矩阵才可以利用GPU的并行性来提高计算速度。

class LinearModel(torch.nn.Module):  
    def __init__(self):  
        super().__init__()  
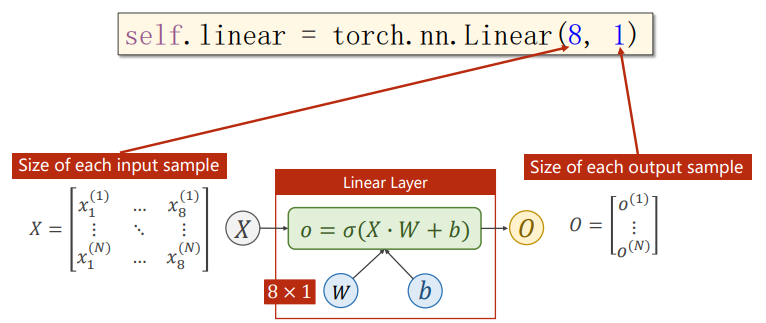
        self.linear = torch.nn.Linear(8, 1)     # 输入8维，输出1维
  
    def forward(self, x):  
        y_pred = torch.sigmoid(self.linear(x))  
        return y_pred

Linear Layer

逻辑斯蒂回归实际上只有一层，尝试增加神经网络层数。

原本输入8维输出1维：

如果把输出维度变为2：

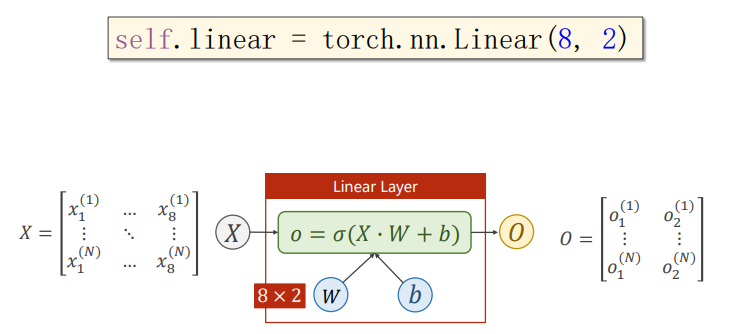
我们需要的输出维度是1维的，那么只需要在后面再加一层输入为2维输出为1维的网络，就可以达到输出为1维的目的。

把输出维度变为6也是同理：

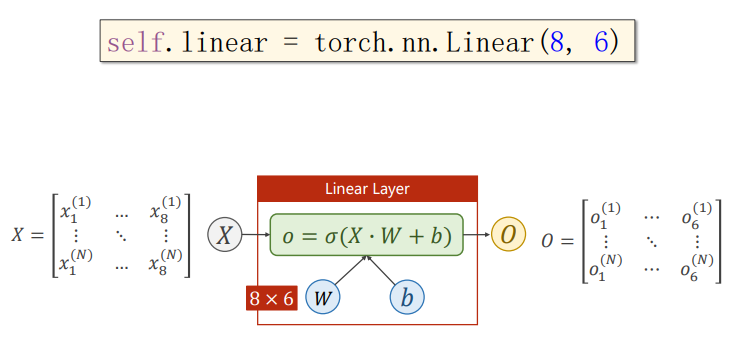
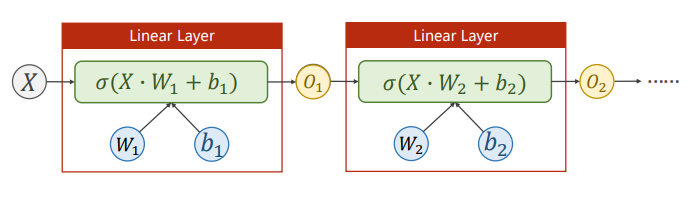
Tips

要记住每次变换都要引入激活函数。通过给线性变换引入非线性的激活函数使得可以拟合非线性的变换。

Tips

层数越多学习能力越强，但是过多的层数更容易发生过拟合。

Implementation

import torch  
import numpy as np  
  
# 数据准备  
xy = np.loadtxt('diabetes.csv.gz', delimiter=',', dtype=np.float32)  
x_data = torch.from_numpy(xy[:, :-1])  
y_data = torch.from_numpy(xy[:, [-1]])  
  
  
# 定义模型  
class Model(torch.nn.Module):  
    def __init__(self):  
        super().__init__()  
        self.linear1 = torch.nn.Linear(8, 6)  
        self.linear2 = torch.nn.Linear(6, 4)  
        self.linear3 = torch.nn.Linear(4, 1)  
  
    def forward(self, x):  
        x = torch.sigmoid(self.linear1(x))  
        x = torch.sigmoid(self.linear2(x))  
        x = torch.sigmoid(self.linear3(x))  
        return x  
  
  
model = Model()  
  
# 构造损失和优化器  
criterion = torch.nn.BCELoss(reduction='mean')  
optimizer = torch.optim.SGD(model.parameters(), lr=0.1)  
  
# 训练周期  
for epoch in range(100):  
    # Forward  
    y_pred = model(x_data)  
    loss = criterion(y_pred, y_data)  
    print(epoch, loss.item())  
  
    # Backward  
    optimizer.zero_grad()  
    loss.backward()  
  
    # Update  
    optimizer.step()